Dale Hoffman
Bellevue College
dhoffman@bellevuecollege.edu
A free on-line calculus text
Many of these materials were developed for the Open Course Library Project of the Washington State Colleges as part of a Gates Foundation grant. The goal of this project was to create materials that would be FREE (on the web) to anyone who wanted to use or modify them (and not have to pay $200 for a calculus book). They have been used by several thousand students.
The textbook sections, in color, are available free in pdf format at the bottom of this page.
Printed versions, in B&W, are available for Calculus I (chapters 0-3), II (chapters 4-8), and III (chapters 9-11) for about $18 each at Lulu.com.
Alternate printed versions reformatted in LaTex are available at CreateSpace.com and Amazon.com or free online at ContemporaryCalculus.com.
The links below are to pdf files. When you click on them, they will be downloaded to your computer. You will need Adobe Acrobat Reader to open them.
Chapter 1 -- Functions, Graphs, Limits and Continuity
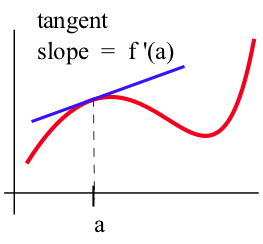
Chapter 2 -- The Derivative
Chapter 3 -- Derivatives and Graphs
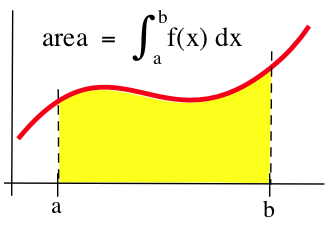
Chapter 4 -- The Integral
Chapter 5 -- Applications of Definite Integrals
Chapter 6 -- Introduction to Differential Equations
Chapter 7 -- Inverse Trigonometric Functions
Chapter 8 -- Improper Integrals and Integration Techniques
This work by Dale Hoffman for Washington State Colleges is licensed under a Creative Commons Attribution 3.0 United States License. You are free to print, use, mix or modify these materials as long as you credit the original to Dale Hoffman. MSWord versions are available from the author.
last modified August 25, 2016